多くの科学現象は移流、拡散、反応によってモデル化され、しばしば非線形拡散方程式や異常拡散方程式によって記述されます。また数理ファイナンスや金融工学などの実社会の様々な問題を考察する際にもこれらの問題が現れることが知られており、近年、応用面からも非常に多くの研究が行われています。計算機の発展に伴い、様々な方法によって微分方程式を解析できるようになってきましたが、拡散方程式などの時間発展する現象を記述する偏微分方程式、すなわち発展方程式によって記述された現象を数学的に理解するためにまず初めにやるべきことは、その問題が時間局所解を持つかを調べることです。その後、時間大域可解性や解の漸近挙動を考察していくことで、問題や方程式に内在する性質を抽出し、現象の理解への足がかりを構築していくことができます。
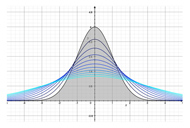
本研究室では関数解析などの数学解析の手法を用いることで、非線形拡散や異常拡散を記述する発展方程式の時間局所及び大域可解性を考察し、それらを足がかりに時間大域解の漸近挙動やその分類、また高次漸近展開を行うことで、解の形状や性質の数学的な解明を目的とします。これらを通して、様々な拡散現象やそこに現れる非線形性の影響の本質的な理解を深めていきます。図は線形熱方程式の基本解であるGauss核の時間変化ですが、多くの典型的な非線形項を有する非線形拡散方程式は初期値が十分小さい場合、その時間大域挙動はこのGauss核の定数倍になります。