- 教員氏名
- 松木平 淳太(まつきだいら じゅんた) 教授
- 学位
- 博士(工学)
- 学歴
- 東京大・院・工
- 専門分野
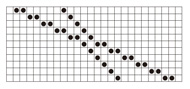
- 非線形波動、ソリトン、可積分系、超離散系、セルオートマトン
- 研究課題(長期)
- 離散系、超離散系に対する数理的枠組の構築
- 研究課題(短期)
- ソリトン系、セルオートマトン系における Euler-Lagrange 対応
龍谷大学 You, Unlimited
Need Help?
Faculty of Advanced Science and Technology
先端理工学部松木平 淳太(まつきだいら じゅんた)

研究テーマ:離散モデルによる現象の解析
近年のコンピュータの計算能力の発達によって、数学的に取り扱いが困難な問題も、数値計算等で近似的に解くことができるようになってきました。しかしながら、デジタル化に伴う離散化誤差は避けることはできず、どの程度の精度で結果が得られているかを常に意識する必要があります。それは現象を正確な把握を目的とする理学の分野のみならず、設計の精度が要求される工学の分野にも当てはまります。ところで水波や光ファイバーの中にはソリトンと呼ばれる安定したパルス波が存在します。ソリトンは衝突によっても壊れることのないという不思議な性質を持っています。長年に渡るこのソリトンの研究の中で、この安定性の背後には「可積分性」と呼ばれる深い数学的な構造があり、それが安定的な数値計算などに関係していることもわかってきました。さらにソリトン・セルオートマトンと呼ばれる 0 と 1 だけで構成される完全に離散的なモデルにも同じ構造が存在することが最近わかってきています。すなわちデジタル化された離散モデルの中にも、数学的に厳密な取り扱いができるものがあるということです。現在我々の研究室では、セルオートマトンと通常の微分方程式や差分方程式系を結ぶ超離散化の研究を精力的に行っています。最近はセルオートマトンによる交通流モデルにおいて、運転者の立場から見たLagrange 的見方と道路管制者側から見たEuler的見方を結びつけることに成功し、さらなる拡張を試みているところです。