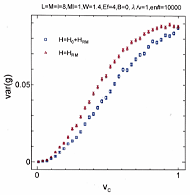
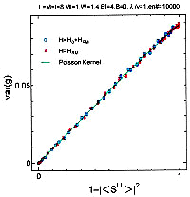
研究課題（短期）の説明の為、障害物が多数ある通路を右に進む波を想像してください。波がある障害物にあたり散乱波ができます。この散乱波が別の障害物や通路の壁にあたると更に散乱波が生じます。こうして波が右に進むにつれ次々と散乱波が生じ、それらの重ね合わせから非常に複雑な波のパターンができるでしょう。このパターンは障害物の位置や通路の形を少しでも変えると不規則に変化し、そこには法則はなにも無い様に思えます。しかし、パターンの集まりの統計的性質、例えばある向きに出る波の平均的な強さなど、については理論式を見出せる場合があります。波の不規則な多重散乱の干渉効果による統計的揺らぎは幅広い自然現象、極低温での電子伝導や複雑な原子核反応など、に現れます。更に、これらの異なる現象の統計的性質が共通性を持つ事が分かってきました。平均などの統計量は少数個のパラメーターを含む普遍的関数で現され、個々の系の特質は全てこのパラメーターに繰り込まれる事が明らかになってきました。右図は大学院生による計算例です。2つのモデルに対して左から入射した波が障害物のある領域を通って右側に透過する割合を縦軸は示しています。上図では横軸はモデルに元々含まれるパラメータを示し、2つのモデルに対して異なる曲線が得られます。一方、横軸をこの系に適切なパラメーターにとり直した下図では２つの曲線が一致し、更にその曲線が理論式（PoissonKernelと記された線）と一致する事がわかります。このような普遍性が現れる理由はなにか？などに興味を持って研究を続けています。